Introdução
- 854
- 23
- Leroy Lebsack
Neste rápido tutorial de modelos e gráficos estatísticos, forneceremos um exemplo de regressão linear simples e aprenderemos como executar essa análise estatística básica de dados. Esta análise será acompanhada por exemplos gráficos, que nos levarão mais perto da produção de gráficos e gráficos com GNU R. Se você não estiver familiarizado com o uso de R, dê uma olhada no tutorial pré -requisito: um rápido tutorial de operações básicas, funções e estruturas de dados.
Modelos e fórmulas em r
Nós entendemos um modelo nas estatísticas como uma descrição concisa dos dados. Essa apresentação de dados é geralmente exibida com um Fórmula matemática. R tem sua própria maneira de representar relacionamentos entre variáveis. Por exemplo, o seguinte relacionamento y = c0+c1x1+c2x2+… +Cnxn+r está em r escrito como
y ~ x1+x2+…+xn,
que é um objeto de fórmula.
Exemplo de regressão linear
Vamos agora fornecer um exemplo de regressão linear para GNU r, que consiste em duas partes. Na primeira parte deste exemplo, estudaremos uma relação entre os retornos do índice financeiro denominado no dólar americano e esses retornos denominados no dólar canadense. Além disso, na segunda parte do exemplo, adicionamos mais uma variável à nossa análise, que são retornos do índice denominado no euro.
Regressão linear simples
Faça o download do arquivo de dados do exemplo para o seu diretório de trabalho: regressão-exemplo-gnu-r.CSV
Vamos agora executar r em Linux a partir da localização do diretório de trabalho simplesmente por
$ R
e leia os dados do nosso arquivo de dados de exemplo:
> retornos<-read.csv("regression-example-gnu-r.csv",header=TRUE) Você pode ver os nomes das variáveis digitando
> Nomes (retornos)
[1] "EUA" "Canadá" "Alemanha"
É hora de definir nosso modelo estatístico e executar a regressão linear. Isso pode ser feito nas seguintes linhas de código:
> y<-returns[,1]
> x1<-returns[,2]
> retornos.LM<-lm(formula=y~x1)
Para exibir o resumo da análise de regressão, executamos o resumo() função no objeto retornado retorna.LM. Aquilo é,
> Resumo (retorna.lm)
Chamar:
lm (fórmula = y ~ x1)
Resíduos:
Min 1q mediana 3q max
-0.038044 -0.001622 0.000001 0.001631 0.050251
Coeficientes:
Estimar std. Erro t valor pr (> | t |)
(Intercept) 3.174E-05 3.862E-05 0.822 0.411
x1 9.275E-01 4.880E-03 190.062 <2e-16 ***
---
Signif. Códigos: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.'0.1 "1
Erro padrão residual: 0.003921 em 10332 graus de liberdade
Múltiplo R-Squared: 0.7776, R-Squared ajustado: 0.7776
F-estatística: 3.612E+04 em 1 e 10332 df, valor p: < 2.2e-16
Esta função gera o resultado correspondente acima. Os coeficientes estimados estão aqui C0~ 3.174E-05 e c1 ~ 9.275E-01. Os valores P acima sugerem que a interceptação estimada C0 não é significativamente diferente de zero, portanto, pode ser negligenciado. O segundo coeficiente é significativamente diferente de zero desde o valor p<2e-16. Therefore, our estimated model is represented by: y=0.93 x1. Além disso, o R-Squared é 0.78, o que significa que cerca de 78% da variação na variável y é explicada pelo modelo.
Regressão linear múltipla
Vamos agora adicionar mais uma variável ao nosso modelo e realizar uma análise de regressão múltipla. A questão agora é se adicionar mais uma variável ao nosso modelo produz um modelo mais confiável.
> x2<-returns[,3]
> retornos.LM<-lm(formula=y~x1+x2)
> Resumo (retorna.lm)
Chamar:
lm (fórmula = y ~ x1 + x2)
Resíduos:
Min 1q mediana 3q max
-0.0244426 -0.0016599 0.0000053 0.0016889 0.0259443
Coeficientes:
Estimar std. Erro t valor pr (> | t |)
(Intercept) 2.385E-05 3.035E-05 0.786 0.432
x1 6.736E-01 4.978E-03 135.307 <2e-16 ***
x2 3.026E-01 3.783E-03 80.001 <2e-16 ***
---
Signif. Códigos: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.'0.1 "1
Erro padrão residual: 0.003081 em 10331 graus de liberdade
Múltiplo R-Squared: 0.8627, R-quadrado ajustado: 0.8626
F-estatística: 3.245e+04 em 2 e 10331 df, valor p: < 2.2e-16
Acima, podemos ver o resultado da análise de regressão múltipla após adicionar a variável x2. Esta variável representa os retornos do índice financeiro no euro. Agora obtemos um modelo mais confiável, já que o R-Squared ajustado é 0.86, que é maior que o valor obtido antes igual a 0.76. Observe que comparamos o R-Squared ajustado porque leva o número de valores e o tamanho da amostra em consideração. Novamente, o coeficiente de interceptação não é significativo; portanto, o modelo estimado pode ser representado como: y = 0.67x1+0.30x2.
Observe também que poderíamos ter se referido aos nossos vetores de dados por seus nomes, por exemplo
> LM (retorna $ USA ~ Retorna $ Canadá)
Chamar:
LM (Fórmula = retorna $ USA ~ Retorna $ Canadá)
Coeficientes:
(Intercept) retorna $ Canadá
3.174E-05 9.275E-01
Gráficos
Nesta seção, demonstraremos como usar r para visualização de algumas propriedades nos dados. Ilustraremos números obtidos por funções como trama(), boxplot (), Hist (), QQNorm ().
Plotagem de dispersão
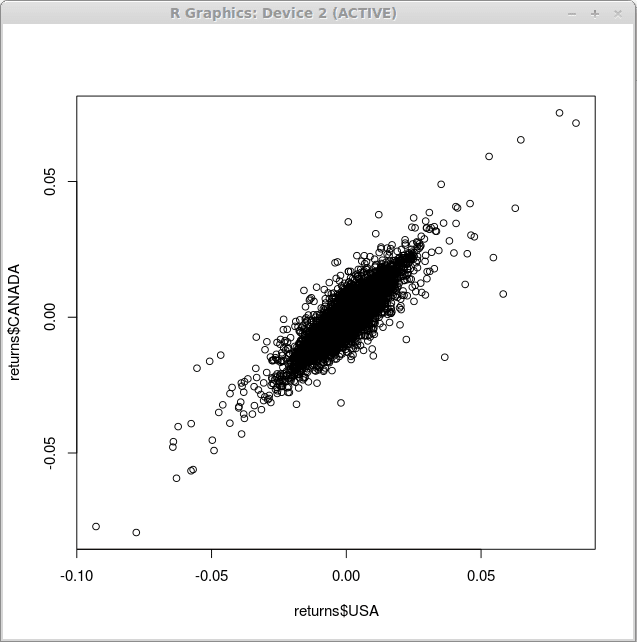
Provavelmente o mais simples de todos os gráficos que você pode obter com r é o enredo de dispersão. Para ilustrar a relação entre a denominação em dólar dos EUA dos retornos do índice financeiro e a denominação do dólar canadense, usamos a função trama() do seguinte modo:
> plot (retorna $ EUA, retorna $ Canadá)
Como resultado da execução desta função, obtemos um diagrama de dispersão, conforme exibido abaixo

Um dos argumentos mais importantes que você pode passar para a função trama() é 'tipo'. Determina que tipo de enredo deve ser desenhado. Os tipos possíveis são:
• '”p“'Para *p *oints
• '”eu“'Para *l *innes
• '”b"' para ambos
• '”c“'Para as linhas, parte de'” B ”'
• '”o“'Para ambos'*o*verso '
• '”h“'Para'*h*istogram 'como (ou' alta densidade ') linhas verticais
• '”s“'Para escada *S *teps
• '”S“'Para outro tipo de *s *teps
• '”n“'Sem trama
Para sobrepor uma linha de regressão sobre o diagrama de dispersão acima, usamos o curva() função com o argumento 'add' e 'col', que determina que a linha deve ser adicionada ao gráfico existente e à cor da linha plotada, respectivamente.
> curva (0.93*x, -0.1,0.1, add = true, col = 2)
Consequentemente, obtemos as seguintes mudanças em nosso gráfico:
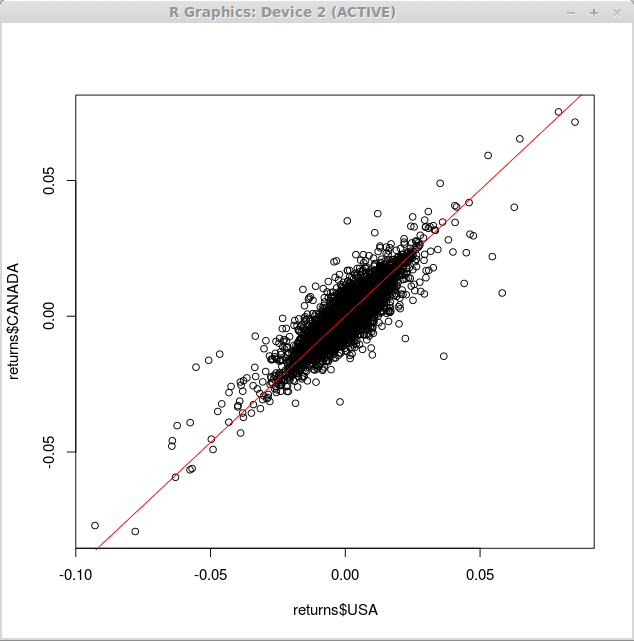
Para obter mais informações sobre a função plot () ou linhas () de uso ajuda(), por exemplo
> Ajuda (lote)
Lote de caixas
Vamos agora ver como usar o boxplot () função para ilustrar a estatística descritiva de dados. Primeiro, produza um resumo das estatísticas descritivas para nossos dados pelo resumo() função e depois execute o boxplot () função para nossos retornos:
> Resumo (retornos)
EUA Canadá Alemanha
Min. : -0.0928805 min. : -0.0792810 min. : -0.0901134
1º Qu.: -0.0036463 1º Qu.: -0.0038282 1º Qu.: -0.0046976
Mediana: 0.0005977 mediana: 0.0005318 Mediana: 0.0005021
Média: 0.0003897 média: 0.0003859 Média: 0.0003499
3º Qu.: 0.0046566 3º Qu.: 0.0047591 3º Qu.: 0.0056872
Máx. : 0.0852364 máx. : 0.0752731 máx. : 0.0927688
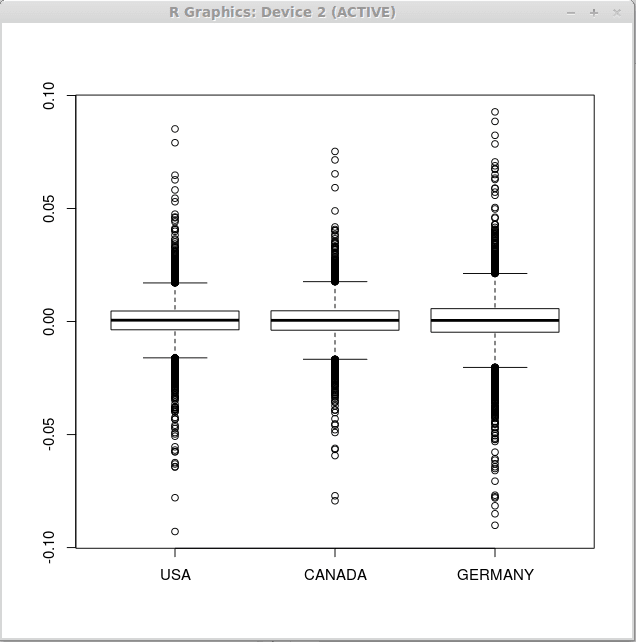
Observe que as estatísticas descritivas são semelhantes para todos os três vetores; portanto, podemos esperar gráficos de caixa semelhantes para todos os conjuntos de retornos financeiros. Agora, execute a função boxplot () da seguinte maneira
> boxplot (retorna)
Como resultado, obtemos os três aparelhos seguintes.
Histograma
Nesta seção, vamos dar uma olhada nos histogramas. O histograma de frequência já foi introduzido em Introdução ao GNU r no sistema operacional Linux. Agora produziremos o histograma de densidade para retornos normalizados e o compararemos com a curva de densidade normal.
Vamos, primeiro, normalizar os retornos do índice denominados em dólares americanos para obter média zero e variação igual a uma para poder comparar os dados reais com a função de densidade normal padrão teórica.
> Retus.norma<-(returns$USA-mean(returns$USA))/sqrt(var(returns$USA))
> Mean (Retus.norma)
[1] -1.053152E-17
> var (Retus.norma)
[1] 1
Agora, produzimos o histograma de densidade para esses retornos normalizados e traçamos uma curva de densidade normal padrão sobre esse histograma. Isso pode ser alcançado pela seguinte expressão r
> Hist (Retus.norma, quebras = 50, freq = false)
> curva (dnorm (x),-10,10, add = true, col = 2)
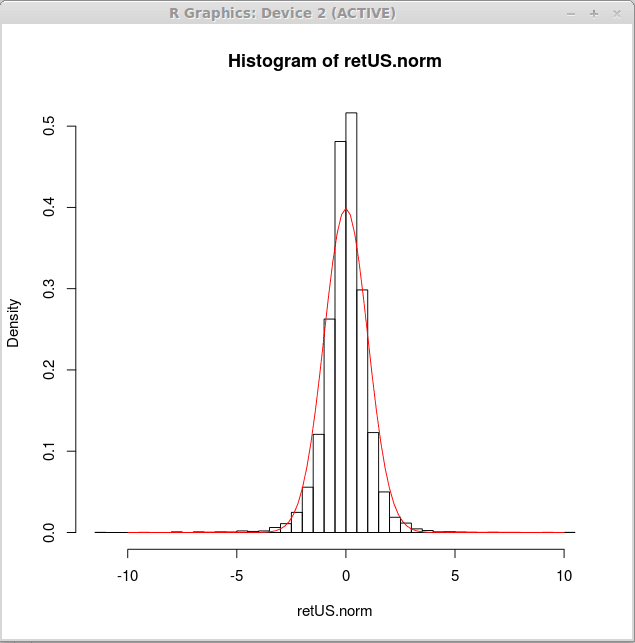
Visualmente, a curva normal não se encaixa bem nos dados. Uma distribuição diferente pode ser mais adequada para retornos financeiros. Aprenderemos como ajustar uma distribuição aos dados em artigos posteriores. No momento, podemos concluir que a distribuição mais adequada será mais escolhida no meio e terá caudas mais pesadas.
QQ-PLOT
Outro gráfico útil em análise estatística é o QQ-Plot. O gráfico qq é um gráfico quantil quantil, que compara os quantis da densidade empírica com os quantis da densidade teórica. Se estes corresponderem bem, deveríamos ver uma linha reta. Vamos agora comparar a distribuição dos resíduos obtidos por nossa análise de regressão acima. Primeiro, obteremos um plot QQ para a regressão linear simples e depois para a regressão linear múltipla. O tipo de plotagem QQ que usaremos é o plano qq normal, o que significa que os quantis teóricos no gráfico correspondem a quantis da distribuição normal.
O primeiro gráfico correspondente aos resíduos de regressão linear simples é obtido pela função qqnorm () Da seguinte maneira:
> retornos.LM<-lm(returns$US~returns$CANADA)
> QQNorm (retorna.LM $ resíduos)
O gráfico correspondente é exibido abaixo:
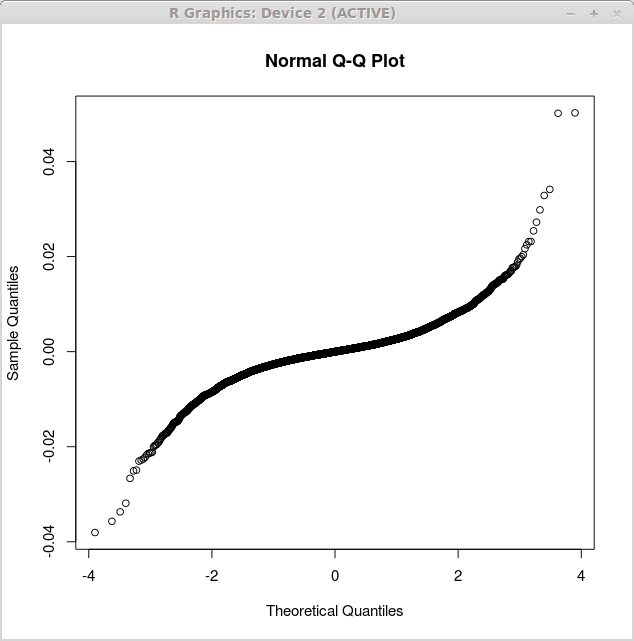
O segundo gráfico corresponde aos múltiplos resíduos de regressão linear e é obtido como:
> retornos.LM<-lm(returns$US~returns$CANADA+returns$GERMANY)
> QQNorm (retorna.LM $ resíduos)
Este gráfico é exibido abaixo:
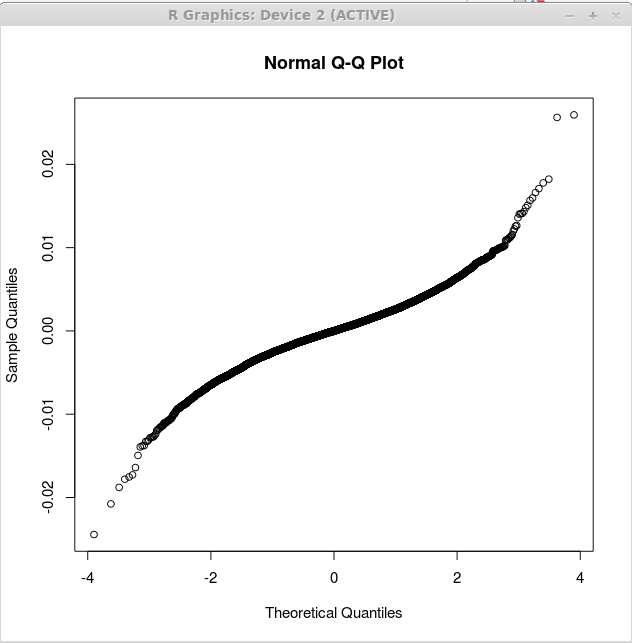
Observe que o segundo lote está mais próximo da linha reta. Isso sugere que os resíduos produzidos pela análise de regressão múltipla estão mais próximos de normalmente distribuídos. Isso suporta ainda mais o segundo modelo como mais útil em relação ao primeiro modelo de regressão.
Conclusão
Neste artigo, introduzimos a modelagem estatística com GNU r no exemplo de regressão linear. Também discutimos alguns usados com frequência em gráficos de estatísticas. Espero que tenha aberto uma porta para a análise estatística com o GNU R para você. Em artigos posteriores, discutiremos aplicativos mais complexos de R para modelagem estatística e programação, portanto, continue lendo.
GNU R R Series:
Parte I: GNU r R Tutoriais introdutórios:
- Introdução ao GNU r no sistema operacional Linux
- Executando o GNU r no sistema operacional Linux
- Um rápido tutorial do GNU R para operações básicas, funções e estruturas de dados
- Um rápido tutorial do GNU R para modelos estatísticos e gráficos
- Como instalar e usar pacotes no GNU r
- Construindo pacotes básicos no GNU r
Parte II: Idioma GNU r:
- Uma visão geral da linguagem de programação GNU R
Tutoriais do Linux relacionados:
- Uma introdução à automação, ferramentas e técnicas do Linux
- Coisas para instalar no Ubuntu 20.04
- Mastering Bash Script Loops
- Coisas para fazer depois de instalar o Ubuntu 20.04 fossa focal linux
- Loops aninhados em scripts de basquete
- Mint 20: Melhor que o Ubuntu e o Microsoft Windows?
- Manipulando a entrada do usuário em scripts bash
- Ubuntu 20.04 truques e coisas que você pode não saber
- Manipulação de big data para diversão e lucro Parte 1
- Ubuntu 20.04 Guia

