Computer Math Basics Binário, Decimal, Hexadecimal, Octal
- 3677
- 268
- Enrique Crist
Como expressamos um número depende se somos um computador ou um humano. Se somos humanos, é provável que expressemos números usando nosso familiar 10-BASE sistema decimal. Se somos um computador, provavelmente somos, em nossa essência, para expressar números como 2-BASE ou binário.
Então, o que há com todas as muitas maneiras de expressar números e por que eles existem? Este artigo entrará em alguns detalhes e, esperançosamente, no final você estará contando octal nos seus dedos. O que funciona bem por sinal, desde que você use apenas 8 dedos, afinal ... octal é 8-BASE.
Neste tutorial, você aprenderá:
- Como fazer uma contagem simples em sistemas não decimais, como binário, hexadecimal e octal.
- Quais os termos 2-Base, 10-Base etc. significa e como entendê -los mais facilmente.
- A conexão entre esses vários métodos de expressar números
Computer Math Basics: binário, decimal, hexadecimal, octal Requisitos de software e convenções usadas
| Categoria | Requisitos, convenções ou versão de software usada |
|---|---|
| Sistema | Independente da distribuição Linux |
| Programas | Linha de comando Bash, sistema baseado em Linux |
| Outro | Qualquer utilidade que não esteja incluída no shell bash por padrão pode ser instalada usando sudo apt-get install utility-name (ou yum install para sistemas baseados em redhat) |
| Convenções | # - requer que o Linux -Commands seja executado com privilégios de raiz diretamente como usuário root ou por uso de sudo comando$-exige que o Linux-Commands seja executado como um usuário não privilegiado regular |
Decimal
Estamos todos super familiarizados com o sistema decimal: 1 a 10 ou melhor 0 a 9, O próprio sistema que pensamos desde o primeiro dia da escola e mesmo antes por nossos pais. Mas este sistema numérico não é tudo o que existe. É apenas um deles. Chamamos este sistema em particular 10-BASE como tem uma base de 10 caracteres, ou seja, 0 a 9.
Em decimal, podemos contar facilmente simplesmente usando o que pensamos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 9.
Não precisamos exercer esforço para isso, e vem naturalmente. No entanto, se você realmente pensar sobre isso, não há conexão lógica real entre o número da palavra "zero" e "um" e "um" e "dois" e assim por diante. Claro, com o tempo entendemos que 0+1 = 1 e 1+1 = 2, Mas não há verdadeiro e substancial outro conexão entre um e dois, 1 e 2. É apenas uma forma de expressão.
Para exemplificar isso, considere as afirmações acima em comparação com um fictício 5-BASE sistema. É muito mais difícil para nossas mentes, pois eles não foram treinados no mesmo, para contar em um sistema de 5 bases. Vamos tornar um passo mais difícil e afirmar que nossos 5 números são expressos como (, ), +, = e . respectivamente. Vamos contar para 11, vamos?
0: (1 :) 2: + 3: = 4: . 5 :) (6 :)) 7 :)+ 8 :) = 9 :). 10: +(11: +)
À esquerda, temos números decimais de 10 bases, à direita, temos nosso sistema numérico de 5 bases gerado contando da mesma maneira (e tanto a esquerda quanto a direita têm valores numéricos iguais, I I.e. 10 em decimal/10-base é +( em nosso sistema numérico de 5 bases!).
Eu posso contar com muita facilidade dessa maneira, pois estou muito acostumado a como X-Base Sistemas funcionam. Se você olhar um pouco mais perto da contagem, descobrirá rapidamente como ela funciona e verá como isso se compara bastante ao nosso sistema de contagem baseado em decimal. A pista é essa; Depois de ficar sem personagens, você simplesmente prefixo o primeiro personagem com o primeiro personagem, fazendo dois personagens. Ainda assim, como você escreveria 100? Você tem que trabalhar até a lista? Provavelmente como nossas mentes não são usadas para enumerar as coisas usando esses símbolos.
Nossas mentes entendem decimais e lutam com a maioria dos outros X-Base sistemas numéricos baseados em que x não é 10. Talvez um exemplo? Calcule )) (((A ==-() b… (+ onde usamos A para indicar multiplicação e B é simples vantagem. Mas não há nada parecido nisso, certo? Ainda assim, se convertermos isso em decimais e nosso familiar + e x Símbolos, provavelmente não encontraríamos essas equações para.
Agora que estamos armados com uma compreensão do que X-Base realmente é, o resto é muito mais fácil. E eu prometo: não há mais símbolos estranhos para expressar números, bem, até chegarmos ao hexadecimal 😉
Binário
Até que os computadores quânticos atingem nossas lojas de computadores locais, nossos computadores são bastante limitados. A única coisa, em seu âmago, que um computador entende é poder ou nenhum poder. Nada mais! Um computador simplesmente entende energia ou sem energia, mas não "entender" Que personagem a é, ou que dígito 9 é. Todas essas coisas, e muito mais (eu.e. todo o código do computador) em seu núcleo é expresso de tanta potência ou sem energia.
Uma única unidade de armazenamento e expressão é chamada de pedaço. Um pouco é o núcleo de nível mais baixo, unidade de armazenamento de um computador. A pedaço pode armazenar apenas um único 0 ou um único 1. Na verdade, ele não pode nem armazenar um zero ou um, só pode armazenar energia (nosso 1), ou nenhum poder (nosso 0). Você pode começar a ver como funciona 2-BASE ou binário: ele tem apenas duas expressões: 0 e 1, Sem poder ou poder.
Se você imaginar isso em termos de hardware físico do computador, poderá imaginar uma unidade de disco rígido do tipo mais antigo como uma placa cheia de muitos pequenos lugares que têm energia (são magnetizados) ou não têm energia (não são magnetizados). Se você imaginá -lo como dados que fluem sobre um cabo, poderá imaginá -lo como energia ou sem energia.
Então, vamos fazer a mesma contagem para 11, mas desta vez usando nossos únicos dois métodos possíveis de expressão, os números em nosso sistema numérico binário: 0 e 1.
0: 0 1: 1 2: 10 3: 11 4: 100 5: 101 6: 110 7: 111 8: 1000 9: 1001 10: 1010 11: 1011
À esquerda, temos 10-Base Decimal e, à direita, temos 2-Base Binária.
Uma vez que você Veja, É fácil contar: basta começar com 0 e 1 e observar como 0 sempre tem um significado especial: quando você vier para 2 em decimal, não é 01 (eu.e. o primeiro personagem usado como um novo personagem mais à esquerda), mas sim 10 Como 0 tem o valor real de zero. Em outras palavras, você não escreveria: 0, 1, 2, 3,…, 8, 9, 00 ou 01, como nenhum deles faz sentido; um escreveria 10. O mesmo se aplica aqui.
O mesmo foi o caso em nosso sistema de 5 bases acima: usamos ) ( para expressar o próximo passo depois que todos os nossos dígitos foram usados, e não (( o que seria incorreto. Seria como escrever 00 em vez de 6.
Depois de conhecer essas etapas básicas que se aplicam a todos os sistemas X-Base, fica mais fácil contar. E você pode usar continue adicionando um personagem mais à esquerda e redefinir o personagem mais à direita atualmente em uso, sempre que ficar sem as próximas etapas numéricas usando apenas o comprimento que você tem no momento. Leia algumas vezes as etapas binárias e veja a progressão, e logo você poderá contar com o binário, mesmo sem usar os dedos. Se você usar dedos, lembre -se de usar apenas dois.
Hexadecimal
Então agora que exploramos 10-Base, 2-Base (e 5-Base 😉 Vejamos algo que pode parecer estranho novamente à primeira vista: 16-BASE. Como caberíamos 16 possíveis combinações numéricas em um único personagem? Bem -vindo ao hexadecimal, que usa cartas.
Vamos fazer uma contagem simples primeiro: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
16 caracteres no total, o sistema hexadecimal usa A-F assim que fica sem maneiras de expressar o próximo número nas séries. Contar de um a 11 como fizemos anteriormente seria discutível aqui, pois lá 11 é simplesmente expresso por 'B'. Então, vamos começar um pouco mais adiante no processo desta vez:
0: 0 1: 1… 9: 9 10: a… 15: F 16: 10 17: 11
À esquerda, temos 10-Base Decimal e, à direita, temos 16-Base Hexadecimal. Portanto, é mais fácil lembrar, observe que o Hexa-DeCimal nos faz pensar em 6-10.
Ai! Agora acabamos com 10 em 16 bases hexadecimal, realmente vale a pena 16 em 10-Base Decimal! Isso pode ser um pouco confuso e pode -se ver imediatamente a necessidade de entender claramente com que sistema numérico estamos trabalhando para evitar erros caros.
Muitas calculadoras em vários sistemas operacionais têm um desenvolvedor ou configuração baseada em computador que pode ser ativada para funcionar com diferentes sistemas numéricos. Alguns vão um passo adiante e mostram muito claramente para que o número em mãos se traduziria em vários outros sistemas numéricos da X-Base, como esta grande calculadora incluída no Linux Mint 20:
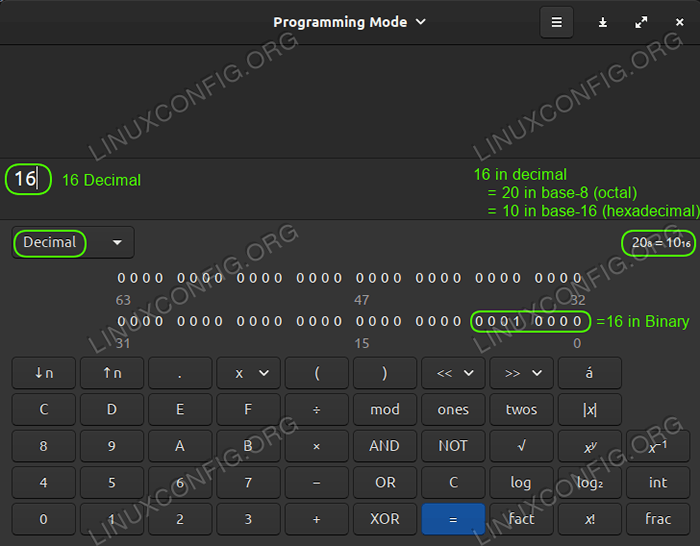Calculadora Linux Mint 20 mostrando decimal, binário, hexadecimal, octal de uma só vez Octal
Agora que vimos os sistemas numéricos anteriores, é mais fácil ver como podemos contar em um sistema de 8 bases, neste caso sendo octal, Outro sistema usado em conjunto com e por sistemas de processamento de computador.
Em Octal, temos 8 caracteres numéricos sendo 0, 1, 2,…, 6, 7. Vamos contar para 11 em um sistema numérico de 8 bases, a partir de 7:
7: 7 8: 10 9: 11 10: 12 11: 13
À esquerda, temos 10-Base Decimal e, à direita, temos 8-Base Octal.
Mais uma vez, podemos ver um um pouco confuso 10 no ser decimal de 10 bases 12 em 8-base octal.
Por que tantos sistemas numéricos?
Então, por que existem tantos sistemas numéricos diferentes? O motivo é simples. Lembre -se de como um pouco era uma loja para colocar um zero binário ou um? Bem, se você pegar 8 bits, terá um byte, e um byte é frequentemente usado para expressar um simples único byte alfa-numérico caracteres. Se você pensar em como o 8 realmente está na base disso, não deve ser muito longe para ver octal (8) se encaixando nos sistemas numéricos sendo usados em computadores.
Em seguida, temos hexadecimal, que é realmente 2 x 8 = 16 caracteres. E aqui, temos 16 bits (ou 2 bytes) representados como um único caractere. Tudo fica de perto e realmente entra em jogo quando você considera como os caracteres alfa-numéricos são usados e processados dentro de sistemas de computador. Por exemplo, alguns personagens especiais (como por exemplo, caracteres japoneses ou chineses) podem exigir que dois ou três bytes os armazenassem (multi-bytes).
Vários sistemas numéricos simplificam os muitos tipos de fluxos de dados que acontecem dentro de um computador e, dependendo dos fluxos em questão, e qualquer algoritmos de computador correspondentes selecionados ou usados, várias otimizações são possíveis dependendo do sistema numérico que você emprega. A maioria dos idiomas em desenvolvimento tem, por exemplo, um processamento binário e potencialmente hexadecimal altamente otimizado, além do processamento decimal.
Conclusão
Neste artigo, mergulhamos em sistemas numéricos 2-BASE, 10-BASE, 16-BASE e 8-BASE, sendo binários (2), decimais (10), hexadecimais (16) e octal (8). Vimos que tipo de conexões existem entre estes e como fazer uma contagem simples em todos esses sistemas.
Aprender um pouco mais sobre como os computadores funcionam geralmente ajuda, especialmente quando se trata de fazer programas de computador ou teoria da compreensão. Quando alguém se torna um desenvolvedor em tempo integral, nesse estágio, todos esses sistemas são uma segunda natureza e são frequentemente usados no código real.
Deixe -nos um comentário com suas idéias sobre esses sistemas numéricos! E se você estiver pronto para aprender coisas mais interessantes, dê uma olhada em nossa manipulação de big data para diversão e lucro na parte 1 artigo! Aproveitar!
Tutoriais do Linux relacionados:
- Tutorial de depuração do GDB para iniciantes
- Uma introdução à automação, ferramentas e técnicas do Linux
- Coisas para instalar no Ubuntu 20.04
- Mint 20: Melhor que o Ubuntu e o Microsoft Windows?
- Sistema Linux Hung? Como escapar para a linha de comando e…
- Coisas para fazer depois de instalar o Ubuntu 20.04 fossa focal linux
- Como fazer cálculos decimais em bash usando BC
- Mastering Bash Script Loops
- Ubuntu 20.04 Guia
- Coisas para fazer depois de instalar o Ubuntu 22.04 Jellyfish…